A Deep Learning Approach for Objective-Driven All-Dielectric Metasurface Design
原创作者:胡铁 纳米光子实验室 目前研究方向:介质偏振计
——||背景介绍||——
2019年11月18号,马萨诸塞州洛厄尔大学的Sensong An和华东师范大学的Jun Ding等人在ACS Photonics发表了题为《A Deep Learning Approach for Objective-Driven All-Dielectric Metasurface Design》的文章。超表面能在波长或者亚波长尺度内调控光的振幅,相位,偏振态等信息,但传统的超表面正向设计,如等效介质理论、迭代数字全波仿真、遗传拓扑优化等,往往耗费极大的计算资源,对超表面的研究和实际应用产生了阻碍。在该论文中,作者提出了一种学习网络,该网络能极大地提升超表面器件设计的速度。与其他拓朴优化算法或者神经网络结合,该方法能在全电磁谱内设计出广泛的多功能超表面器件。
——||创新点||——
该论文提出一种新颖的神经网络。为了解决输入与输出数据维度不匹配问题,论文中提出了一种深度预测神经网络(deep predicting neural network,PNN),该网络采用了改进的神经张量网络(Neural Tensor Network ,NTN),将双线性张量层替换为第一标准线性神经网络层,直接将多维上的两个实体矢量相关联,从而可以通过非线性而不是仅隐式地将两个输入相乘;为了解决相位预测准确度低的问题,论文中对超表面的单元结构的电场响应的实部和虚部数据进行训练,从而解决了由于谐振效应导致π相位突变的问题。首次证明了能够在宽光谱范围内快速准确地预测超表面单元结构的幅度和相位响应的预测神经网络,基于这种高精确的前向预测神经网络,构建了对应于不同设计目标(如基于超表面的光学滤波器)的逆向设计模型,说明其多功能性。
——||理论公式||——
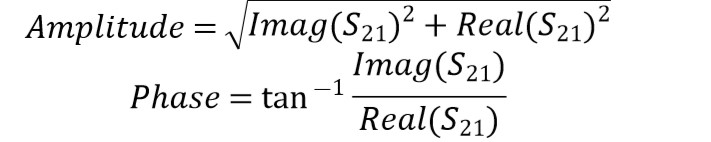
单元结构的电场响应的实部和虚部与其透过系数,相位关系:
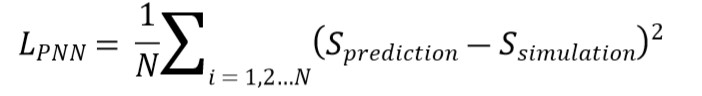
用于PNN的损失函数,是L2损失函数,即LS,
由于基于超表面的滤波器加工和实际应用限制,改进的损失函数如下:
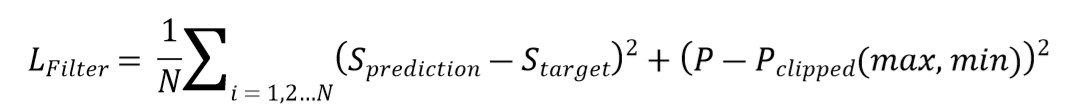
其中,P是包含设计参数的输出向量,向量  是P中所有值均裁剪为预设的最大值和最小值的向量。
是P中所有值均裁剪为预设的最大值和最小值的向量。

用来评估训练结果的误差是分数差异,即:
——||图文一览||——

图一:PNN的模型与结构
(a) 超表面单元结构数值仿真得到的相位(蓝色)和振幅响应。设计参数在右侧表中列出。相位跳变(黑色虚线圆圈)代表电磁多偶极子引入的π相位不连续性。
(b) 和图(a)相同单元结构的电场响应的实部和虚部。
(c) 单元结构的示意图,PNN的输入参数,包括折射率、间隙距离、高度和圆柱体半径。
(d) PNN的主要网络结构示意图。包括两层独立的全连接层,每个包含四个隐藏层,分别构造为预测复数透射系数的实部和虚部。 蓝色圆圈代表输入参数,灰色圆圈代表隐藏的神经元,红色圆圈代表输出值。
(e) PNN提供的离散实部和虚部数据的一个样本。
(f) 通过内插离散输出样本(红点)来重建连续数据(蓝色曲线)。
(g) 相应的透过系数曲线和相位曲线。
小结:为了不失一般性和实际加工的简易性,PNN的训练数据几何形状采用圆柱体,从相位和透过率的光谱响应曲线可以明显发现在谐振处有明显的突变,而其对应的电场实部和虚部响应连续,因此针对电场电场的实部和虚部响应设计了两个独立PNN网络。该方法不仅能提升相位预测的准确度,还能降低输出数据维度。与简单地连接实体向量的标准神经网络相比,改进NTN可以乘法地关联两个输入,而不是仅通过非线性来隐式关联。
图二:PNN网络性能示例证明
左侧所示的小插图是每个单元结构透过系数的实部和虚部。大子图中显示的红色曲线表示相位曲线,而蓝色曲线表示幅度响应。点表示由PNN生成的数据,而实曲线是从数值模拟获得的数据。插图中按以下顺序给出了每个单元结构的设计参数:介电常数,间隙,高度和半径(以微米为单位)。从测试数据中随机选择四个单元结构。
小结:共50000组数据用于PNN的训练,在网络训练完成后,对于实部整体测试均方误差为0.00035,对于虚部整体测试均方误差为0.00023,幅度和相位响应的分数误差均为0.5%。
图三:用于复杂几何结构的PNN
(h) H型结构的俯视图。
(b-d)由PNN(点)和数值模拟(线)预测的H形单元结构的EM响应示例。单元结构设计参数按以下顺序作为插图给出:介电常数,高度,Lx,Lx1,Ly和Ly1(以微米为单位)
小结:在经过14800组H形单元结构数据集的训练后,PNN能够实现99.4%的幅度预测精度和99.3%的相位预测精度。这些准确的预测结果进一步验证了所提出的方法不限于某些输入/输出大小或某些结构形状。
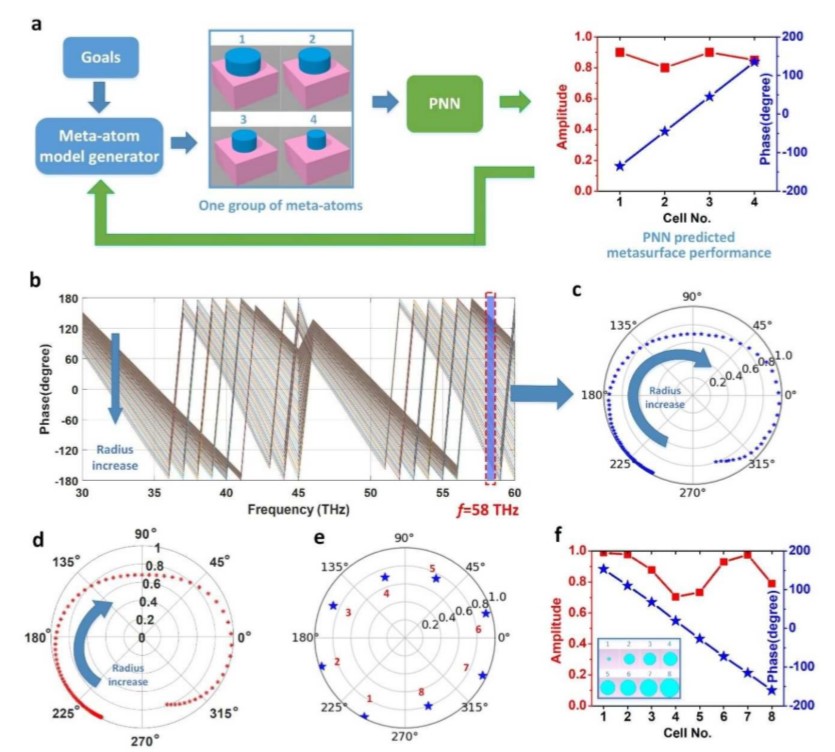
图四:针对特定功能的目标单元结构设计网络和设计实例
(a) 闭环单元结构设计网络的流程图。由模拟生成器生成的设计通过级联的PNN进行评估,矩形图中所示的预测EM响应随后被发送回设计生成器。然后给出新的设计,以最小化当前结果与设计目标之间的差异。
(b) PNN预测的目标单元结构设计在频谱上的相位分布。所有93个设计的晶格尺寸为1.23 m,厚度为1.5 m,而半径则以5 nm的增量在0.1 m至0.56 m之间变化。
(c) PNN预测的目标频率(58 THz)下的相位和幅度曲线。
(d) 以供验证的数值模拟结果
(e) 从具有不同半径(100、315、370、410、445、475、505和560 nm)的模拟数据中选出八个单元,以形成一类3Bit超表面(相位步长为45度)。
(f) 这八个单元的性能和俯视图(插图)。
小结:为了满足特定的应用需求,采用闭环设计网络,而不是构造单个级联的逆设计神经网络。与图4d中数值仿真结果相比,再次显示了PNN的准确性。 高于预设幅度阈值的330度相位覆盖范围可实现3Bit超表面的设计,相邻单元之间的相位差为45度,使用所提出的方法仅需22秒,而在相同的硬件和环境设置下,仅这些设计的数值验证(如图4d所示)就花费了30分钟以上。常规方法达到此设计将花费数小时或数天。
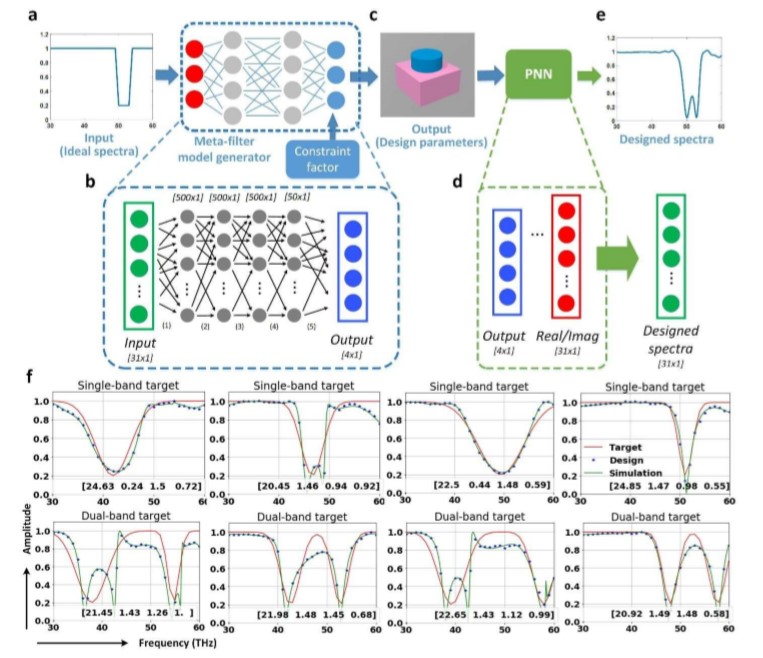
图五:目标超滤波器的逆向设计
(a) 输入的目标光谱。
(b) 使用DNN构建的超滤波器设计网络的模拟生成器。 绿色单元格代表输入,而灰色和蓝色单元格分别代表隐藏的神经元和输出。
(c) 模拟生成器的输出,它是设计参数(例如介电常数和超原子尺寸)的组合。
(d) 然后将这些参数输入到PNN中以产生复数传输系数。
(e) 由复数传输系数得出的生成设计的精细幅度响应。
(f) 来自目标的超滤波器设计网络的几个设计示例,涉及单频段设计目标(第一行)和双频段设计目标(第二行)。红色曲线是目标滤波器的光谱响应,蓝色曲线是基于设计网络给出的设计的PNN预测的滤波器光谱响应,绿色曲线是CST模拟的幅度响应。插图中给出了每种设计的介电常数,间隙,高度和半径。
小结:原则上,功能齐全的超滤器设计网络应该能够生成性能用户自定义的滤光器光谱响应的单元结构。 为了实现此目标,论文中采用经过全面训练的PNN连接到超滤波器模拟生成器以形成级联网络,并避免了由非唯一解引起的非收敛问题。在对每组数据进行50000次训练之后,对于单波段目标和双波段目标,误差最终分别稳定在10.24%和32.05%。由于随机生成的目标光谱可能在物理上是不现实的,因此这些稳定的误差值表明训练已完成。单波段目标的相对较大的误差,甚至双波段目标的较大误差,并不能说明论文中的DNN方法的限制。相反,它证明了无法通过简单的圆柱状全介质单元结构来实现复杂的滤波器功能。
——||结论||——
总之,该论文提出了一种新颖的基于DNN的数据驱动方法,用于快速,准确地表征全介质超表面器件的设计。首次在毫秒时间内准确预测出3D全介质单元结构的幅度和相位响应。进一步研究表明,可以基于此快速而准确的预测神经网络构造超表面器件的逆设计模型。尽管该论文主要讨论了工作于红外光谱下的全介质超表面器件的正向建模和逆设计实例,但该论文提出的用于目标驱动设计的深度学习方法并不局限于此。
文献链接:An S, Fowler C, Zheng B, et al. A Deep Learning Approach for Objective-Driven All-Dielectric Metasurface Design[J]. ACS Photonics, 2019.
DOI:10.1021/acsphotonics.9b00966
