Spin-decoupled multifunctional metasurface

for asymmetric polarization generation

Yuehong Xu, Quan Li, Xueqian Zhang, Minggui Wei, Quan Xu, Qiu Wang, Huifang Zhang, Wentao Zhang, Cong Hu, Zhenwei Zhang, Cunlin Zhang, Xixiang Zhang, Jiaguang Han, and Weili Zhang

——||背景介绍||——

最近具有偏振自由度的多功能超表面因为其具有偏振相关的调控能力受到了广泛的关注。但是设计上有一些困难，如使用吸收或反射式的超表面结构的话，会有一半的入射能量被浪费。不仅如此，这种超表面还能够实现偏振控制，同时通过使极化波偏离零阶输出，可以实现无背景极化。然而，先前报道的基于圆偏振的复用超表面的偏振产生通常由于单一的几何相位而使两个偏转光束具有对称的极化响应，即两束偏转光束的偏振态相同。打破这种极化响应需要额外的自由度，即不对称极化产生，这对于实现功能复杂的新型极化器件非常有用。

——||创新点||——

本文提出了一种简单的方法，利用介质超表面的高效率和较大的相位调整范围来实现自旋解耦太赫兹相位控制。设计了一种将不同圆偏振光偏转成非对称角度的多功能光栅，并对其进行了实验，验证了该方法的有效性。作者把它表示为非对称自旋解耦光栅 (ASM)。接下来，他们将此方法应用于不对称极化产生的复用技术，设计了一组复用性非对称自旋解耦光栅(MASMs)。每一层都是由两个具有互变相位梯度和不同输出相位的层组成。在线偏振入射下，超表面可以将其转换成两种强度相近但方向角不同的线偏振波，并将其偏转到不同的角度。为了验证这一方法，作者选择了一个有代表性的MASM并进行了实验验证。他们所提出的光栅拓宽和深化了超表面的应用，并可应用于特定的极化相关系统。

——||基本原理||——

f和s代表硅柱的两个对称方向，那么在fs坐标下一个硅柱的传输矩阵如下：

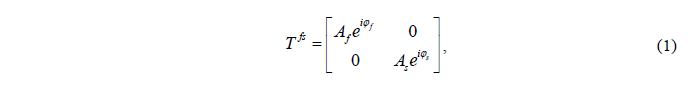
那么在xy坐标系下，透过率可以表示如下：

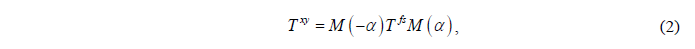
然后将xy坐标系转换为圆坐标系，透过率可以表示如下：

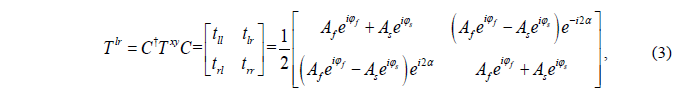
其中 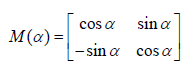是xy和fs两个坐标系的旋转矩阵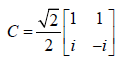， 是从圆坐标系到xy坐标系的转换矩阵。+2α和−2α都知道是几何相位，其实它整体还和前面结构的动态相位相关。

考虑一个特殊的例子Af = As = A and φs – φf = π，即单元结构类似半波片功能，则（3）可以改写为如下：

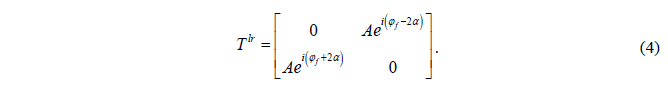
可以实现完美的偏振转换功能，相位变化取决于动态相位和几何相位共同作用。

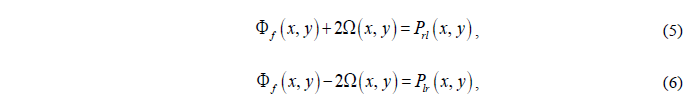
可以看出动态相位对两种出射光的相位作用相同，几何相位作用相反，且独立不影响，便于设计。

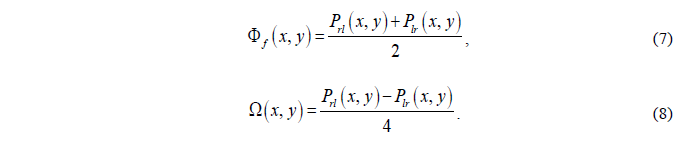
对于另一个动态相位，可以依据半波片的功能给出如下：

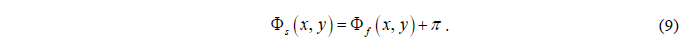
到这里，即将需要设计的出射光的相位分布转变为了单元结构自身的动态相位分布以及旋转的几何相位分布，不仅更利于选取单元结构的尺寸，也更复合仿真结果的表示方法。

接下来通过仿真数据库中选取 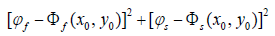最小的结构，同时保证 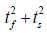最大。接下来旋转每个结构的角度，提供相应的几何相位。

——||图文一览||——

图一：非对称自旋解耦光栅以及结构设计示意图

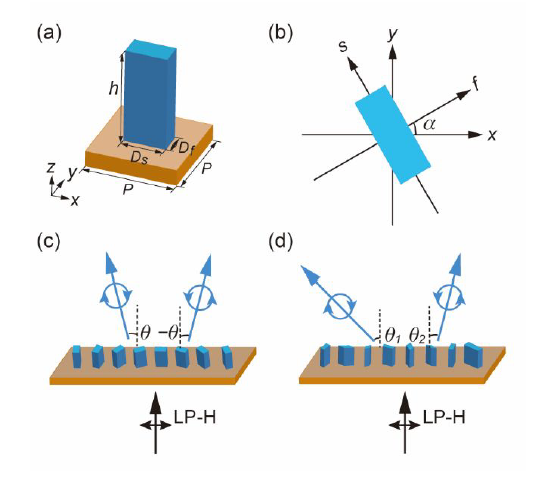
(a) 单元结构示意图，硅衬底上摆放矩形的硅柱；

(b) 单元结构旋转示意图，旋转角为短轴与x轴正方向的夹角；

(c) 基于几何相位的传统光栅示意图，仅仅只能将正入射的线偏光分解为沿着对称角度出射的两束圆偏光；

(d) 基于动态相位和几何相位的非对称自旋解耦光栅示意图，能够将左旋光和右旋光沿着不同角度出射。

小结：结构的周期P选的150μm，高度h选的200μm，D_f和D_s在20μm到140μm之间变化，以提供0到2π的相位覆盖。

图二：非对称自旋解耦光栅的仿真示意图

(a)理论（实线和虚线）以及仿真（空心三角）的相位分布，以及相应的仿真（空心矩形）透射振幅分布，前面一个字母代表入射圆偏光的偏振态，后面一个字母代表出射圆偏光的偏振态；

(b, c) 分别是在LCP和RCP入射时出射光的RCP和LCP的场强分布，上方区域代表结构，白色虚线为出射光的波矢方向，波长为1Thz ；

(d, e) 分别是在LCP和RCP入射时出射光的RCP和LCP的模拟角分布；

小结：仿真设计时Prl = 2πx/nlP + φ0， Plr =−2πx/nrP + φ0。将nl = 6, nr = 8代入，沿x方向选取24个单元结构。理论上的两种光偏转角度如下，实验上测量的角度为19.84°和-14.03°，与理论吻合的很好，相关转换效率分别为60.97%和61.02%。

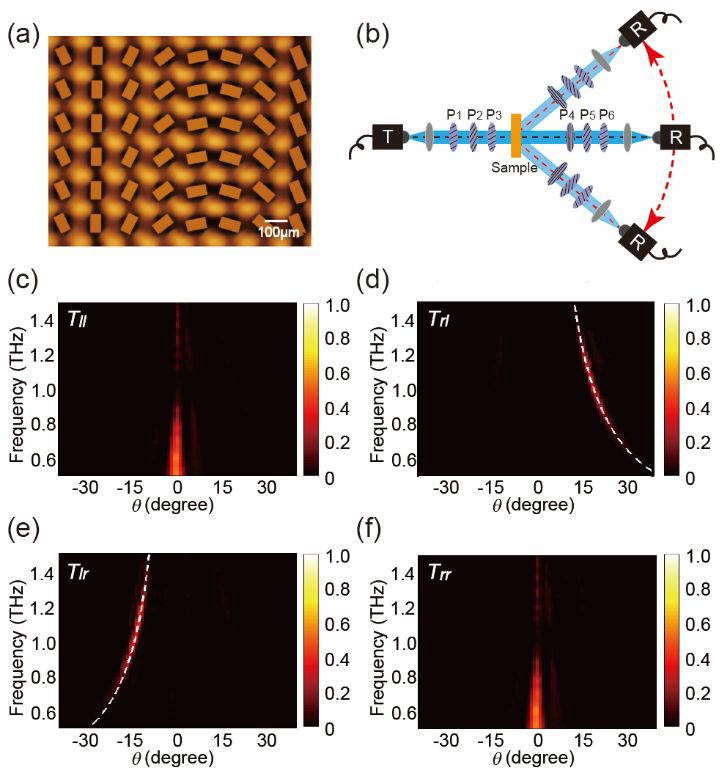
图三：非对称自旋解耦光栅的实验结果

(a) 制造的非对称自选解耦光栅的局部显微镜图像；

(b) 实验光路示意图；

(c-f) 测量的宽带不同圆偏光透过率和出射角，d和e中的白色虚线代表根据广义斯涅尔定律计算出来的偏转角度和频率之间的关系。

小结：先测得线偏光入射时的相关透射率t_xx, t_xy, t_yy, t_yx, 然后将其转换为圆偏振光下的透射率t_ll, t_lr, t_rl, t_rr, 仿真波长从0.6Thz到1.4Thz，测得的偏转效率基本为30%。

图四：多路复用非对称自旋解耦光栅的设计示意图以及相关仿真结果

(a) 多路复用非对称自旋解耦光栅的设计思路，由两个不同的ASM组成；

(b-e) 理论（实线和虚线）和仿真（空心三角）的相位分布图以及ASM-B的仿真（空心矩形和圆）振幅分布；ASM-A的相位和振幅分布都与图二一样。

(f-i)  在x偏光入射时的相关仿真结果，上面的代表在θ₁和θ₂处的偏振态；

小结：ASM-B具有与ASM-A相同效率，但是偏转方向不同。

PrlB = PlrA − Δφ2 = Plr − Δφ2 PlrB = PrlA + Δφ1 =Prl + Δφ1

所以ASM-B出射光的偏转角只是与ASM-A发生了翻转。然后整体上会有一个叠加作用。

如果入射线偏光的偏振态旋转θ，那么在两个角度的叠加偏振态也会旋转θ。

图五：对所设计的MASM进行实验验证

(a) 制造的多路复用非对称自选解耦光栅的局部显微镜图像；

(b-e) 测量的宽带不同偏振光透过率和出射角；

(f-i) 测量的宽带不同偏振光透过率和出射角，白色虚线代表根据广义斯涅尔定律计算出来的偏转角度和频率之间的关系。

(j-m) 提取出来的两个角度处的透过率。

——||结论||——

作者提出了一种自旋解耦相位控制方法，将动态相位和几何相位相结合，利用太赫兹范围内全硅介质超标表面实现自旋解耦相位控制。然后他们进一步应用一种多路复用的方法来产生不对称极化，它可以在线性极化入射下产生任意不同偏角的线性极化。该方法基于介电超表面平台，打破限制之前的多路复用超光栅极化唯一的几何相位,并提出新的潜在途径来调节产生偏振,因此在各个领域有潜在应用,包括超全息、偏振光束分割和偏振复用系统。虽然它只在太赫兹范围内被证明，但可以很好地扩展到电磁频谱的其他频率范围。